Energy Minimization with Linear Smoothness Term: A Proof of Uniqueness of Solution for an Undirected Graph Formulation
tech-report » diromartin-trudeau , Sébastien Roy
Mots-clés: champs aléatoires de Markov , discontinuités de profondeur , maximum-flow , MRF , stéréo
Date : 2001-02
Résumé
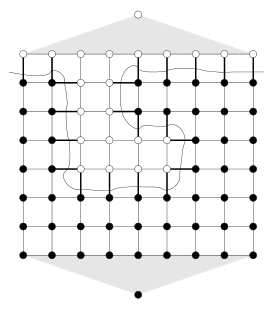Recently many graph theoretic formulations where proposed for solving specific energy functions minimization problems. The specific case where a linear penalty term is used to enforce smoothness is of particular interest since it makes it possible to find the global solution using an efficient flow algorithm in a graph. However, a proof was needed to establish equivalence between a minimum s-t cut of a simple undirected graph and the original minimization problem. This paper presents such a proof for very general graphs, thereby making unnecessary the workarounds used until now, while providing some performance enhancement. Extending on previous one-dimensional proof, it is general enough to allow arbitrary graphs of any dimension as well as arbitrary neighborhood structure.
Documents
