Graph cut: Application to Bayesian Emission Tomography Reconstruction
conference » iciapjean-meunier , Martin Bonneville , Sébastien Roy
Mots-clés: champs aléatoires de Markov , MRF , reconstruction volumétrique , stéréo , tomographie
Date : 1999-09
Résumé
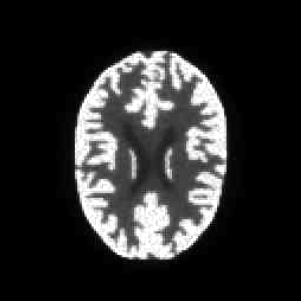 We present an application of graph cuts to Bayesian emission tomography (ET) reconstruction. The method is built on the expectation-maximization (EM) maximum a posteriori (MAP) reconstruction. In general, MAP estimates are hard to assess. For instance, methods such as simulated annealing cannot be employed, because of the computational complexity of bayesian ET reconstruction. We propose to perform a part of the M-step by a maximum-flow computation in a particular flow graph. Because the possible priors (in a maximum-flow approach) are limited to linear function, we have incorporated the estimation of a line process that will preserve discontinuities in the reconstructions. It is the iterative nature of EM that allows the introduction of the line process. The method is illustrated first over synthetic data and then over the Hoffman brain.
We present an application of graph cuts to Bayesian emission tomography (ET) reconstruction. The method is built on the expectation-maximization (EM) maximum a posteriori (MAP) reconstruction. In general, MAP estimates are hard to assess. For instance, methods such as simulated annealing cannot be employed, because of the computational complexity of bayesian ET reconstruction. We propose to perform a part of the M-step by a maximum-flow computation in a particular flow graph. Because the possible priors (in a maximum-flow approach) are limited to linear function, we have incorporated the estimation of a line process that will preserve discontinuities in the reconstructions. It is the iterative nature of EM that allows the introduction of the line process. The method is illustrated first over synthetic data and then over the Hoffman brain.